|
Exponents and Logs
Identify the principal amount:
A = 235(1 + 0.025)t

Identify the principal amount:
A = 235(1 + 0.025)t

Identify the rate as a percent:
A = 235(1 + 0.025)t

Identify the rate as a percent:
A = 235(1 + 0.025)t

Does the following equation represent a growth or decay function? How do you know?
y = 226(1.037)t

Does the following equation represent a growth or decay function? How do you know?
y = 226(1.037)t

You put $250 in a savings account. It gains 3.8% interest compounded annually. How much money will the savings account have in 5 years?

You put $250 in a savings account. It gains 3.8% interest compounded annually. How much money will the savings account have in 5 years?

Your juice contains a toxic substance. It is decreasing at a rate of 8.5% per hour. After 11 hours, what percent of the substance will remain?

Your juice contains a toxic substance. It is decreasing at a rate of 8.5% per hour. After 11 hours, what percent of the substance will remain?

Does the graph below represent exponential growth or decay?


Does the graph below represent exponential growth or decay?


Draw an example of an exponential decay graph.


Draw an example of an exponential decay graph.


What is the starting value (A) of the decay function below?


What is the starting value (A) of the decay function below?


Approximately what is the Count Rate of sodium at 60 hours?


Approximately what is the Count Rate of sodium at 60 hours?


Do growth and decay functions (like those pictured below) ever hit zero? Why or why not?
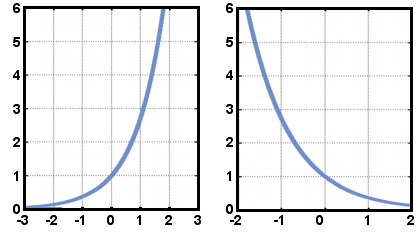

Do growth and decay functions (like those pictured below) ever hit zero? Why or why not?

No. The rate only takes a percentage of the starting value, never all of it.

Identify the base.
log5x = 1

Identify the base.
log5x = 1

Identify the exponent.
log35 = 2x

Identify the exponent.
log35 = 2x

Write in exponential form.
logx = 3

Write in exponential form.
logx = 3

Write a logarithmic form.
24x = y

Write a logarithmic form.
24x = y

What two logarithmic properties are demonstrated below?
log34x + log37x = 120
log328x2 = 120
2log328x = 120

What two logarithmic properties are demonstrated below?
log34x + log37x = 120
log328x2 = 120
2log328x = 120
Product Property & Power Property

Expand.
log24x

Expand.
log4x6

Expand.
logx2y6

Condense.
log5x + log52x

Condense.
3log3x - 2log3x

Condense.
3log3x - 2log3x

Solve for x.
log2x7 = 21

Solve for x.
log6(x - 4)2 = 2

Solve for x.
log6(x - 4)2 = 2

Solve for x.
log10x + log104 = 1

Solve for x.
log10x + log104 = 1

Solve for x.
logx - log9 = 5

Solve for x.
logx - log9 = 5

Solve for x.
log26 + log2(x - 6) = 1

Solve for x.
log26 + log2(x - 6) = 1

Given a decay rate of 12 percent, write the equation of the line below:


Given a decay rate of 12 percent, write the equation of the line below:



| Team 1 |
 |
|
 |
|
| Team 2 |
 |
|
 |
|
| Team 3 |
 |
|
 |
|
| Team 4 |
 |
|
 |
|
| Team 5 |
 |
|
 |
|
| Team 6 |
 |
|
 |
|
| Team 7 |
 |
|
 |
|
| Team 8 |
 |
|
 |
|
| Team 9 |
 |
|
 |
|
| Team 10 |
 |
|
 |
|

What Would You Like To Risk?

| Team 1 |
 |
|
 |
|
| Team 2 |
 |
|
 |
|
| Team 3 |
 |
|
 |
|
| Team 4 |
 |
|
 |
|
| Team 5 |
 |
|
 |
|
| Team 6 |
 |
|
 |
|
| Team 7 |
 |
|
 |
|
| Team 8 |
 |
|
 |
|
| Team 9 |
 |
|
 |
|
| Team 10 |
 |
|
 |
|
Go To The Final Question
Final Score:

| Team 1 |
 |
|
 |
|
| Team 2 |
 |
|
 |
|
| Team 3 |
 |
|
 |
|
| Team 4 |
 |
|
 |
|
| Team 5 |
 |
|
 |
|
| Team 6 |
 |
|
 |
|
| Team 7 |
 |
|
 |
|
| Team 8 |
 |
|
 |
|
| Team 9 |
 |
|
 |
|
| Team 10 |
 |
|
 |
|

Edit This Game:

|
|


