|
Quadrilaterals
I'm a quadrilateral whose diagonals bisect each other. Who am I?

I'm a quadrilateral whose diagonals bisect each other. Who am I?
parallelogram

I'm a quadrilateral with only one pair of opposite parallel sides. Who am I?

I'm a quadrilateral with only one pair of opposite parallel sides. Who am I?
Trapezoid

I'm a quadrilateral with congruent diagonals. Who could I be?

I'm a quadrilateral with congruent diagonals. Who could I be?
rectangle, square, isosceles trapezoid

I'm a quadrilateral whose diagonals are perpendicular. Who could I be?

I'm a quadrilateral whose diagonals are perpendicular. Who could I be?
rhombus, square

Both pairs of my opposite sides are parallel. My diagonals bisect the angles, but my diagonals are not congruent. Who am I?

Both pairs of my opposite sides are parallel. My diagonals bisect the angles, but my diagonals are not congruent. Who am I?
Rhombus

In the parallelogram below, find the measure of the missing angles. 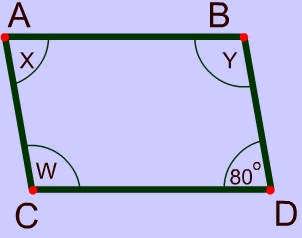

In the parallelogram below, find the measure of the missing angles. 
X = 80, W = Y = 100

Find the value of x. 

Find the value of x. 
x = 10

In rectangle ABCD, AB = 5x + 17 and CD = 4x + 29.5. Find the measure of AB.

In rectangle ABCD, AB = 5x + 17 and CD = 4x + 29.5. Find the measure of AB.
mAB = 79.5

In rectangle ABCD, diagonals AC and BD intersect at E. If AE = 7x+ 3 and BE = 10x - 21, find the value of x.

In rectangle ABCD, diagonals AC and BD intersect at E. If AE = 7x+ 3 and BE = 10x - 21, find the value of x.
x = 8

You are asked to prove quadrilateral MATH is a parallelogram but not a rectangle. Explain one way you can go about this proof.

You are asked to prove quadrilateral MATH is a parallelogram but not a rectangle. Explain one way you can go about this proof.
You can show both pairs of opposite sides are congruent to prove it is a parallelogram. To show it is not a rectangle, calculate the distance of the diagonals and show they are not equal.

Find the measure of AC in the rhombus below. 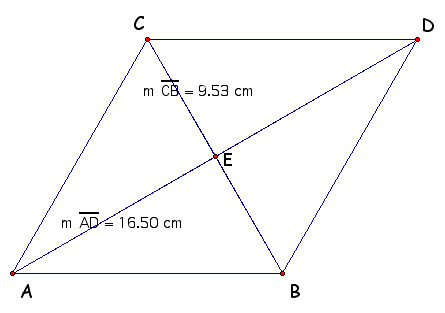

Find the measure of AC in the rhombus below. 
mAC = 9.5

In square BLUE, diagonals BU and EL intersect at C. What is the measure of angle BLC?

In square BLUE, diagonals BU and EL intersect at C. What is the measure of angle BLC?
45. angle BLU = 90 and the diagonals bisect the angles, so angle BLC = 45.

Explain why the parallelogram below is NOT a rhombus. 

Explain why the parallelogram below is NOT a rhombus. 
In the parallelogram, the diagonals do not bisect the angles.

In square DRAW, the measure of DR = 15. Find the measure of diagonal DA.

In square DRAW, the measure of DR = 15. Find the measure of diagonal DA.
15radical2 (15 square root of 2)

You are trying to prove CARD is a rhombus but not a square. Explain how you could go about doing this.

You are trying to prove CARD is a rhombus but not a square. Explain how you could go about doing this.
Show all four sides are congruent to prove CARD is a rhombus. However, when you calculate the distances of the diagonals, they will not be equal, hence proving quadrilateral CARD is not a square.

Explain the difference between a trapezoid and a parallelogram.

Explain the difference between a trapezoid and a parallelogram.
In a trapezoid, exactly one pair of opposite sides is parallel. In a parallelogram, both pairs of opposite sides are parallel.

In isosceles trapezoid CODE, CO || DE. If OD = 63 and CE = 5x + 3, find the value of x.

In isosceles trapezoid CODE, CO || DE. If OD = 63 and CE = 5x + 3, find the value of x.
x = 12

In the isosceles trapezoid below, d = 10, a = 20, and b = 32. Find the value of h. 

In the isosceles trapezoid below, d = 10, a = 20, and b = 32. Find the value of h. 
h = 8

In trapezoid BATH, BA || TH and m angle B = 100. Find m angle H.

In trapezoid BATH, BA || TH and m angle B = 100. Find m angle H.
m angle H = 80. Same side interior angles are supplementary.

Using coordinate geometry, explain how to prove quadrilateral KITE is an isosceles trapezoid.

Using coordinate geometry, explain how to prove quadrilateral KITE is an isosceles trapezoid.
Calculate the slopes of all four sides to show exactly one pair of opposite sides is parallel. Then, either calculate the length (using the distance formula) of the legs (non-parallel sides) or the diagonals and show they are equal in measure.

If the diagonals of a quadrilateral do not bisect each other, then the quadrilateral could be a (1) rectangle (2) rhombus (3) square (4) trapezoid

If the diagonals of a quadrilateral do not bisect each other, then the quadrilateral could be a (1) rectangle (2) rhombus (3) square (4) trapezoid
(4) trapezoid

In isosceles trapezoid ABCD, AB is congruent to CD. If BC = 20, AD = 36, and AB = 17, what is the length of the altitude of the trapezoid? (1) 10 (2) 12 (3) 15 (4) 16

In isosceles trapezoid ABCD, AB is congruent to CD. If BC = 20, AD = 36, and AB = 17, what is the length of the altitude of the trapezoid? (1) 10 (2) 12 (3) 15 (4) 16
(3) 15

In parallelogram STUV, SV = x + 3, VU = 2x - 1, and TU = 4x - 3. What is the length of SV? (1) 5 (2) 2 (3) 7 (4) 4

In parallelogram STUV, SV = x + 3, VU = 2x - 1, and TU = 4x - 3. What is the length of SV? (1) 5 (2) 2 (3) 7 (4) 4
(1) 5

The coordinates of the vertices of parallelogram ABCD are A(-3, 2), B(-2, -1), C(4, 1), and D(3, 4). The slopes of which line segments could be calculated to show that ABCD is a rectangle? (1) AB and DC (2) AB and BC (3) AD and BC (4) AC and BD

The coordinates of the vertices of parallelogram ABCD are A(-3, 2), B(-2, -1), C(4, 1), and D(3, 4). The slopes of which line segments could be calculated to show that ABCD is a rectangle? (1) AB and DC (2) AB and BC (3) AD and BC (4) AC and BD
(2) AB and BC

Quadrilateral ABCD with AB congruent to CD and AD congruent to BC, and diagonal BD is drawn. Prove angle BDC is congruent to angle ABD.

Quadrilateral ABCD with AB congruent to CD and AD congruent to BC, and diagonal BD is drawn. Prove angle BDC is congruent to angle ABD.
Answer is a proof

When a quadrilateral is reflected over the line y = x, which geometric relationship is not preserved? (1) congruence (2) orientation (3) parallelism (4) perpendicularity

When a quadrilateral is reflected over the line y = x, which geometric relationship is not preserved? (1) congruence (2) orientation (3) parallelism (4) perpendicularity


| Team 1 |
 |
|
 |
|
| Team 2 |
 |
|
 |
|
| Team 3 |
 |
|
 |
|
| Team 4 |
 |
|
 |
|
| Team 5 |
 |
|
 |
|
| Team 6 |
 |
|
 |
|
| Team 7 |
 |
|
 |
|
| Team 8 |
 |
|
 |
|
| Team 9 |
 |
|
 |
|
| Team 10 |
 |
|
 |
|

What Would You Like To Risk?

| Team 1 |
 |
|
 |
|
| Team 2 |
 |
|
 |
|
| Team 3 |
 |
|
 |
|
| Team 4 |
 |
|
 |
|
| Team 5 |
 |
|
 |
|
| Team 6 |
 |
|
 |
|
| Team 7 |
 |
|
 |
|
| Team 8 |
 |
|
 |
|
| Team 9 |
 |
|
 |
|
| Team 10 |
 |
|
 |
|
Go To The Final Question
Final Score:

| Team 1 |
 |
|
 |
|
| Team 2 |
 |
|
 |
|
| Team 3 |
 |
|
 |
|
| Team 4 |
 |
|
 |
|
| Team 5 |
 |
|
 |
|
| Team 6 |
 |
|
 |
|
| Team 7 |
 |
|
 |
|
| Team 8 |
 |
|
 |
|
| Team 9 |
 |
|
 |
|
| Team 10 |
 |
|
 |
|

Edit This Game:

|
|
















